LAB 6: Non-parametric Tests

In this lab, we will examine:

• Two probability distributions used in non-parametric tests: and D
• How and when to use the following tests:
  • one sample Chi-square
  • two or more sample Chi-square
  • one sample Kolmogorov-Smirnov
  • two sample Kolmogorov-Smirnov
• How to calculate expected frequencies
• Important cautions for the Chi-square tests

Recommended web links:
Hyperstat.com: A diagram of the Chi-square distribution
VassarStats: An applet showing how the Chi-square distribution changes with different degrees of freedom. Enter degrees of freedom in the dialogue box that pops up (between 1 and 20)
Examples and Applications: An overview and examples using the Chi-square distribution
 

Applied hypothesis testing...

There are two groups of inferential statistical tests: parametric and non-parametric tests. A parametric test requires that the underlying population for each sample is normally distributed, and that the data are either interval or ratio.

Non - parametric tests have been developed that use only frequency counts in the calculation of the test statistics. No assumptions are made about the shape of the underlying population distribution.
 

Introduction to Goodness of Fit Tests

'Goodness of Fit' tests compare the frequencies observed in a sample to a distribution of expected frequencies in order to infer similarity.

When we discuss the mechanics of the non-parametric Goodness of Fit tests, you will notice the word distribution used in two different contexts.

1. Frequency distributions refer to the distribution of data values in a sample or population (refresh my memory). The tests use frequencies in different ways:
   • Chi-square() tests use simple frequency counts.
   • Kolmogorov-Smirnov tests use cumulative relative frequencies.
      
     
2. Probability distributions ( and D) model the distribution of test statistics (refresh my memory). Two important probability distributions are introduced below.

The Chi-square () Distribution

Pronounced kai not chee   This distribution begins at 0 and is positively skewed   The distribution has no negative values.	Shape of the distribution
There are many distribution shapes, each associated with a different number of degrees of freedom (similar to the student’s t distribution). As the number of degrees of freedom increases, the distribution becomes less skewed   This distribution is used for the one and multi-sample Chi-square tests.

The ‘D’ Distribution

• The D distribution has a similar shape to the distribution.
   
  
• This distribution also starts at 0 and has no negative values.
   
  
• The D distribution is used specifically for the Kolmogorov-Smirnov Goodness of Fit test
   
  

Applications and Calculations

These tests use the hypothesis testing procedures detailed in Lab 5. For each test, we will outline:

• the general uses of the test
• how the test works
• the test assumptions
• the appropriate hypotheses
• the appropriate probability distribution
• how to calculate the test statistic
• what is the decision rule
• how to apply the test (using an example)

Chi-square tests

The chi-square tests are the most basic tests because they use nominal categories and simple frequency counts. They are flexible tests because they can be applied to most data. However, these tests treat all categories as nominal so information associated with ordinal, interval or ratio levels of measurement will be lost.

In this discussion, we are going to start with one and two sample chi-square tests and then examine the one and two sample Kolmogorov-Smirnov tests.

One Sample Chi-square () Test

Use

How does it work?

This test uses the following statistical hypotheses:

:	there is no difference between the observed and expected frequencies (i.e. the sample is drawn from a population that follows the expected distribution).
:	there is a significant difference between the observed and expected frequencies (i.e. the sample is drawn from a population that does not follow the expected distribution).

The test statistic provides a measure of the amount of difference between the two frequency distributions. If the difference between the observed and expected distributions is small, will be small. If the difference is large, will be large.

Assumptions

• Data are organized into nominal or ordinal categories. You can ‘downgrade’ interval or ratio data to the ordinal level by collapsing the data into categories.
• Categories are mutually exclusive
• Frequencies are absolute counts (i.e. not relative frequencies or percentages).
• If only two categories, the expected frequency in each must be 5 or more.
• If more than 2 categories, no category should have an expected frequency less than 1, and not more than one in 5 expected frequency counts should be less than 5.

 
Test Statistic

Formula: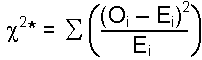

where: Oi = observed frequency in each category Ei = expected frequency in each category

Critical Value

Decision rule

Reject if the calculated value (*) is greater than critical value ().   If the * is greater than , it will fall in the red 'rejection region' on the chi-square probability distribution.

Example

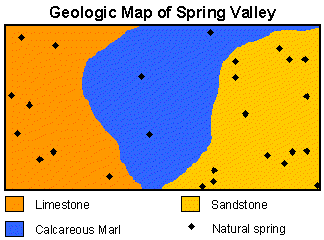
RESEARCH QUESTION: Is the occurrence of natural springs influenced by rock type?

1. Select the appropriate test:
To investigate this research question, we need to compare our observed frequencies to a uniform frequency distribution. Why? If rock type is not important in determining the location of springs, we will expect the number of springs to be evenly distributed over rock type. If our observed frequencies are different from the expected uniform frequencies, we can infer that rock type affects the occurrence of natural springs. We will use the one sample chi-square test to answer our research question.

2. Check assumptions:

• rock types are nominal categories
• categories are mutually exclusive (each rock belongs to one category only)
• frequencies are absolute counts (dataset does not contain relative frequencies)
• expected frequencies:
  To calculate the expected frequencies for a uniform distribution, take the total observed count and divide by the number of categories. In this example, we have observed 24 natural springs in three rock type categories. Therefore, we would expect 24/3 = 8 springs in each category if rock type did not influence the location of springs.
   
  No category has an expected frequency of less than 5
  You can apply this test to your data.

3. State your hypotheses:

: there is no difference between the observed and expected frequencies
: there is a significant difference between the observed and expected frequencies

4. Select significance level:
We will use the standard = 0.05 (95% confidence level)

5. Select probability distribution of test statistic:
This test uses the distribution for the test statistic

6. Establish the critical values:
At = 0.05, and degrees of freedom (k-1) = 2, the critical value () = 5.99.
(Recall that k is the number of categories; we have 3 rock types so k = 3)

7. Calculate test statistic:

Step 1: List the observed and expected frequencies for each category
Step 2: For each category, subtract the expected from the observed, square the result and divide by the expected frequency (see table)
Step 3: Sum the results from Step 2 to get *.

Rock type	Observed frequency	Expected frequency	(Obs-Exp)2/Exp
Limestone	7	8	0.13
Calcareous Marl	3	8	3.13
Sandstone	14	8	4.50
Total	24		7.75

Therefore, * = 7.75

8. Make inference using the decision rule:

Rule: reject if * >   From above, * (7.75) is greater than (5.99), so reject

9. State conclusion:
We conclude with 95% confidence that the observed frequencies are significantly different from the expected (uniform) frequency distribution (i.e the springs are not uniformly distributed between rock types). We infer that rock type influences the occurrence of natural springs in Spring Valley.

Your turn!

Two or more sample Chi-square () test

Uses

How does it work?

This test uses the following hypotheses:

: the samples are drawn from the same parent population (no difference).
: the samples are not drawn from the same parent population (difference).

If there are large differences between the observed and expected frequencies, the * test statistic will be greater than the critical value. Therefore, we will reject and infer that the samples are drawn from different underlying populations. If the differences between the observed and expected frequencies are small, * will be small and we will not reject . In this case, we would infer that the samples are drawn from the same underlying population.

Assumptions

• Data are organized into nominal or ordinal categories
• Each variable has at least 2 mutually exclusive categories
• Frequencies are absolute counts (i.e. not relative frequencies or percentages)
• If two categories, expected frequency in each category must be 5 or more
• If more than 2 categories, no category should have an expected frequency of less than 1 and not more than one in 5 expected frequency counts should be less than 5. Categories or samples can sometimes be combined if the expected frequency counts in some categories are too low.

Probability Distribution

Test Statistic

Formula: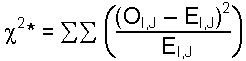

where: Oi,,j = observed frequency in each cell Ei,,j = expected frequency in each cell

Note: the double means sum all rows and columns in the table.

Critical Value

Decision rule

Example

RESEARCH QUESTION: Is there a significant difference between the responses of the user groups?

1. Select the appropriate test:
We need to determine if there are differences between the observed frequencies of 3 samples (user groups). If the responses of the user groups are similar we can infer that the user groups are all part of the same underlying population. If there are differences in the responses, we can infer that the user groups come from different parent populations. We will use the multi-sample test

2. Check assumptions:

• Responses are nominal categories
• Categories are mutually exclusive
• Each sample has 2 or more categories
• Expected frequencies:
  For this test, calculate the frequencies expected in each cell of the contingency table
   
  

  Each cell in the table is referenced as follows:
  
   
  For each cell, the expected frequency (at row I and column J) is:
  
   
  For our data, the expected frequencies are:
  Daily / widen bridge: E_1,1 = (67 * 60)/180 = 22.3
  Commercial / widen bridge: E_1,2 = (67 * 60)/180 = 22.3
  ...
  Commercial / tunnel: E_2,2 = (57 * 60)/180 = 19.0
  ...
  Tourist / transit: E_3,3 = (56 * 60)/180 = 18.7
  

  The observed and expected frequencies are shown in this table:

  Responses	Commuters		Operators		Tourists		Total
  	Obs	Exp	Obs	Exp	Obs	Exp
  Widen	19	22.3	22	22.3	26	22.3	67
  Tunnel	8	19.0	35	19.0	14	19.0	57
  Transit	33	18.7	3	18.7	20	18.7	56
  Total	60		60		60		180

  No expected frequency is less than 5
  we can apply this test.

3. State your hypotheses:

: there is no significant difference between the response of the three user groups
: there is a significant difference between the responses of the three user groups

4. Select significance level:
We will use standard = 0.05 (95% confidence level)

5. Select probability distribution of test statistic:
This test uses the distribution for the test statistic.

6. Identify the critical values:
At = 0.05, degrees of freedom (k-1)*(l -1) = (3-1)*(3-1) = 4, therefore = 9.49. (Recall that k is the number of categories and l is the number of samples)

7. Calculate test statistic:

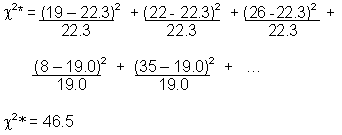
8. Compare using the decision rule:

Rule: reject if * >   From above, 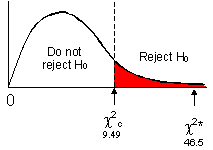* (46.5) is greater than (9.49), so we can reject .

9. State conclusion:
We infer with 95% confidence that there is a significant difference between the responses of the user groups in terms of their preferences of alternatives for the Lions Gate Bridge crossing.
 

Chi-square Cautions

1. The chi-square tests will not work if the expected frequencies are ‘too small’ (see the assumptions for the one and two sample tests). Sometimes categories can be combined to ensure that expected frequencies are large enough. However, this may make no sense within the context of the data available, and you may have to abandon the test.
    
   
2. Although the chi-square tests can be used with any level of measurement (data must be collapsed into categories), these tests treat all categories as nominal. If the categories are ordinal, the chi-square tests disregard this information. If your data are ordinal or higher, it may be better to use a more powerful statistical method. As the Kolmogorov Smirnov test preserves ordering, it is often a good alternative.
    
   
3. As the chi-square tests use absolute frequencies, they do not differentiate between large and small samples when calculating the difference between observed and expected frequencies. A small difference between large frequencies will result in a high * test statistic and you will end up rejecting . A relatively big difference between small frequencies will give a low * and you will not reject .
    
   Example:

   Case	Obs	Exp	Difference	Comments
   A	510	500	10	These frequencies are quite large, so the difference of 10 is relatively minor.
   B	10	5	5	These frequencies are small, so the difference of 5 is very important. The observed frequency is twice as large as the expected.

   In the hypothesis test, you would probably reject in case A (and infer a significant difference) and not reject in case B (and infer no difference). Because the critical value () is based on number of categories and not sample size, the test cannot account for the relative differences in actual frequencies.
    
   Although there are limitations to the chi-square, these tests are easy to use and have many applications, particularly for analyzing survey or social data. In these types of research, the data are usually collected at the nominal scale.
    
   

Kolomogorov-Smirnov Tests

The Kolmogorov-Smirnov (KS) tests also compare observed and expected frequencies. However, these tests are different from the chi-square tests because the KS tests use cumulative relative frequencies in their test statistic. To develop cumulative relative frequencies, the data must be at the ordinal scale. These tests are considered more powerful that the chi-square tests because they use a higher level of measurement. However, the ordinal scale restriction means that the tests cannot be applied as widely as the chi-square tests.

One Sample KS Test

Uses

How does it work?

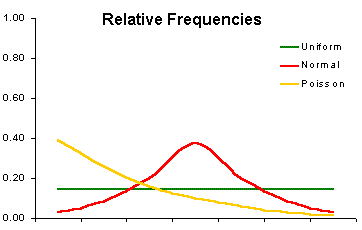
Three ways to display frequencies

Comparing 3 expected distributions

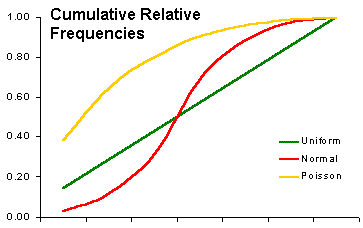
This test compares the two cumulative relative frequencies (CRF) to find the maximum difference between the observed and expected frequencies. The maximum difference is the D* test statistic.

Observed CRF vs 3 Expected CRF
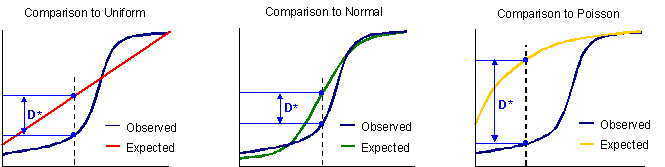
Note: for this example, the observed frequencies have an approximately normal shape with a slight negative skew. Therefore, there is only a small difference between the observed and expected (normal) frequencies.

This test uses the following hypotheses:

:	there is no difference between the observed and expected frequencies (i.e. the sample is drawn from a population that follows the expected distribution).
:	there is a significant difference between the observed and expected frequencies (i.e. the sample is drawn from a population that does note follow the expected distribution).

If the two cumulative relative frequencies are similar, the maximum difference (D) will be small and we cannot reject . We infer that the observed distribution follows the expected distribution. If, however, there is a large difference between the two cumulative relative frequencies (D is large), we reject .

Assumptions

• Observations are independent events at the ordinal scale or higher.
• There must be at least two categories and categories must be mutually exclusive.
   
  Note: SPSS will automatically categorize interval or ratio data when performing the test.

Probability Distribution

Test Statistic

Formula:
	this means "D* is the maximum (or largest) absolute (without + or - sign) difference between the observed cumulative relative frequencies () and the expected cumulative relative frequencies ()"

Critical Value

Decision rule

Example

QUESTION: Are her data normally distributed?

1. Select appropriate test:
We will use the one sample KS test because it will allow us to compare the observed frequencies against the frequencies expected for a normal distribution. This test also allows us to retain the ordinal nature of the data (a chi-square test would convert the ordinal categories to nominal categories, resulting in a loss of information).

2. Check assumptions:

• The ratio data (persons per household) have been collapsed into ordinal categories
• There are 7 mutually exclusive categories
• An expected distribution has been specified (the normal distribution)
  We can apply the KS test to these data

3. State your hypotheses:

: there is no difference between the observed and expected frequencies
: there is a difference between the observed and expected frequencies

4. Select the significance level:
We will use the standard = 0.05 (95% confidence level)

5. Establish the probability distribution of the test statistic:
Because we are conducting a KS test, we use the D distribution for the test statistic.

6. Establish the critical values:
At = 0.05, degrees of freedom (n) = 70, = 0.16

7. Calculate the test statistic:

Step 1: Calculate the cumulative frequencies for the observed distribution () by adding frequencies starting at the lowest category.
 
Step 2: Calculate the observed cumulative relative frequencies () by dividing each by the total number of observations
 
Step 3: Calculate the and for the expected distribution. See notes below for information on expected frequencies.
 
Step 4: Subtract the from the for each category
 
Step 5: Remove the sign (+ or -) from the result to get D
 
Step 6: The largest difference is D*

Category	Observed			Expected			D
1-2	3	3	0.04	2	2	0.03	0.01
3-4	5	8	0.11	7	9	0.13	0.02
5-6	6	14	0.20	13	22	0.31	0.11
7-8	9	23	0.33	26	48	0.69	0.36
9-10	15	38	0.54	13	61	0.87	0.33
11-12	23	61	0.87	7	68	0.97	0.10
13-14	9	70	1.00	2	70	1.00	0.00
Total	70			70

From the table, D* is 0.36

8. Make inference using the decision rule:

Rule: reject if D* >
From above, D* (0.36) is greater than (0.16), so we can reject .

9. State conclusion:
We conclude with 95% confidence the observed frequencies are significantly different from the expected (normal) frequency distribution. Therefore, we infer that the underlying population is not normally distributed and the researcher cannot use parametric tests to analyse these data.
 

Two sample KS test

Use

How does it work?

: there is no difference between the two observed frequencies (i.e. both samples are drawn from the same underyling population)
: there is a difference between the observed frequencies (i.e. the samples are drawn from different underlying populations)

Rejecting follows the same logic given in the one-sample KS test.

Assumptions

• Observations are independent events at the ordinal or higher scale
• There must be at least two categories and categories must be mutually exclusive. Note: SPSS will group ratio or interval data into categories when it performs the KS test

Probability Distribution

Test Statistic

Formula:
	"D* is the maximum absolute difference between the CRF in sample A and the CRF in sample B"

Critical Value

Significance Level ()	Critical D formula
0.10	1.22 *
0.05	1.36 *
0.025	1.48 *
0.01	1.63 *
0.005	1.73 *
0.001	1.95 *

Decision rule

Practice

A regional planner is reviewing the proposed expansion of recreational facilities for two communities. The age structure of each community will influence the type of new or expanded facilities (i.e. daycare and children’s programs or seniors’ activity center). In the past, the two communities had similar demographics. However, recent migration trends may have changed the demographic patterns. Random sampling was conducted in each community; the data are presented below.

RESEARCH QUESTION: Is there a significant difference between the age classes of the two communities? Check your answer.
 

Expected Frequencies

• Uniform: As we saw in the example, the uniform frequencies are calculated by dividing the total frequency by the number of categories.
  Example: Sample A had 150 observations, in 10 categories. The expected frequency for each category is 150/10 = 15.
   
  
• Normal: The normal frequencies used in the KS example were simulated. Developing expected normal frequencies is very complicated and best left to a computer. Therefore, when using the KS to test for normality, you will use SPSS to obtain D*.
   
  
• Poisson: The Poisson distribution is a common frequency distribution, which is used to model the occurrence of rare events within set time period. The calculation of the Poisson frequencies is detailed below.

  To use this distribution, the data must fulfill certain conditions:

  1. The number of events in any time period is independent of the events in another period.
  2. The probability that one event occurs within a time period is low and the probability of multiple events is very low.
  3. The time periods are small compared to the longer overall observation period.
      
     

  Calculating Poisson frequencies is a two step process. The steps are outlined below. Then we will apply these steps to calculate Poisson frequencies for lightning stikes.

  Step 1: Calculate the average number of events () per unit area or block of time
   
  Step 2: Use to calculate the expected Poisson frequencies:

  Formula: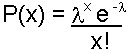

  where x = number of events per time period or unit of space = mean number of events e = 2.71828 (base or natural logarithm)

Example: The number of lightning strikes per day were recorded in Alberta for 6 summers (for months of July and August). The data are presented below.

Strikes per day	Days
0	209
1	115
2	32
3	8
4	1
Total	365

1. A lightening strike on July 26 is independent of a strike on Aug 13 condition satisfied
2. The probability of a single strike in a day is low; the probability of multiple strikes on the same day is very low condition satisfied.
   
3. The daily time period is small compared to the 6 year observation period condition satisfied.

Strikes per day (Xi)	Days (w)	# of strikes
0	209	0 * 209 = 0
1	115	1 * 115= 115
2	32	2 * 32 = 64
3	8	3 * 8 = 24
4	1	4 * 1 = 4
Total	365	207





= 207/365 = 0.567 strikes per day
 

Step a: Calculate e to the power of - (save this number as you will use it several times)
Step b: Calculate to the power of x (where x = number of strikes per day)
Step c: Multiply the results from Steps a and b; divide by x! ('x factorial' - use the n! button on your calculator)

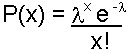
To develop the Poisson frequency distribution, you will perform the same calculation for each category of lightning strikes. Two calculations and the completed table of expected frequencies are shown below.

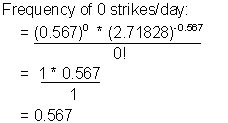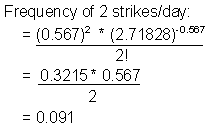
Strikes per day Poisson Probability* Expected Frequencies (Probability x 365 days) 0 0.567 207 1 0.322 118 2 0.091 33 3 0.017 6 4 0.002 .73 Total 1.000 365 *Note: due to rounding, may not add to 1.

For a one sample KS test, the frequencies we calculated above would be used to develop the expected cumulative relative frequencies. The table below shows and for the KS test.

Category (strikes per day)	Observed frequency (days)	Expected Frequency (days)				D
0	209	207	209	0.573	0.567	0.006
1	115	118	324	0.888	0.889	0.001
2	32	33	356	0.975	0.980	0.005
3	8	6	364	0.997	0.997	0.000
4	1	.73	365	1.000	1.000	0.000
Total	365	364.73


 

We can see that the cumulative relative frequencies of lightning strikes observed in Alberta are very similar to the frequencies expected in a Poisson distribution. A significance test would confirm that the observed frequencies are not different from the Poisson distribution. Conduct the test and prove it for yourself (check your answer).

Answers to Practice Questions

One sample test

Critical values:
At = 0.05, and degrees of freedom (k-1) = 3, = 7.82

Test statistic:
* is shown in red.

Decision:
Rule: reject if * >

* (6.00) is less than (7.82), so we cannot reject (we conclude with 95% confidence that the sample is drawn from a population that is significantly different from uniform).
 

Two sample KS test

Critical values:
At = 0.05,

Test statistic:
D* is shown in red.

Decision:
Rule: reject if D* >
From above, D* (0.21) is greater than (0.13), so we can reject (we conclude with 95% confidence that the two samples are drawn from significantly different underyling populations).

One sample KS test with Poisson frequencies

Critical value:
At = 0.05 and degrees of freedom (n = 365), we use the formulas at the bottom of the critical D table to compute the critical value. = 0.071.

Test statistic:
From the lightening strike example, we found that D* was 0.006.

Decision:
Rule: reject if D* >
From above, D* (0.006) is less than (0.071), so we cannot reject (we conclude with 95% confidence that the sample is drawn from a population that is not different from expected - the observed distribution follows the Poisson distribution)