|
|
In this lab, we will examine Difference of Means tests for:
This test calculates the difference between the sample mean (
)
and the population mean (
) and
divides it by the standard error (s/
). The
calculated value of the test statistic tells us how far the sample mean lies
away from the population mean.
The difference of means tests allow us to investigate non-directional and directional hypotheses.
For this test, we can establish the following statistical hypotheses:
 :
| there is no difference between the sample mean and the population mean
( :
= ) |
 :
| there is a significant difference between the sample mean and the population
mean ( :
)
|
The hypotheses as presented above are non-directional because we are interested in whether the sample mean is different from the known value (or population mean), not whether the sample mean is less than or greater than the population mean.
We can establish a directional hypothesis to determine whether the sample mean is greater than or less than the population mean. We would state our hypotheses as follows (shown in text and symbol notation):
| Text | Notation |
|---|---|
| : the sample mean is
not different from (less than or equal to) the population mean.
| :
|
| :
the sample mean is significantly greater than the population mean.
| :
>
|
If the test statistic is a large number, we know there is a large difference
between the sample mean and the known value. In this case, we would reject the
null hypothesis and infer a significant difference between
and . If the test statistic is
a small number, we will not reject the null hypothesis and can infer that there
is no significant difference between and
.
| Formula: | 
| where: is the sample mean is the known or hypothesized population mean s is the sample standard deviation n is the sample size |
probability
is allocated to both sides (tails) of the t-probability distribution. This is
because we are testing only for a difference between
and . The diagram below shows the rejection region associated with
non-directional hypotheses:
|
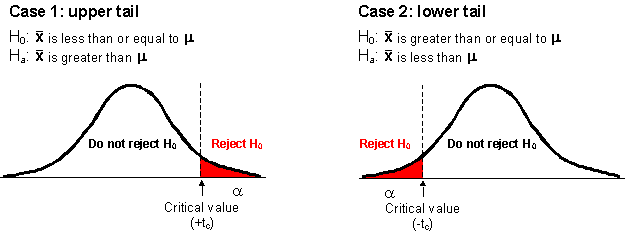
If we established directional hypotheses, and
the rejection region are allocated to one side (tail) of the probability distribution
(Case 1 or Case 2 in the diagram below).
|
/2
for non-directional hypotheses (two tailed test) or
for directional hypotheses (one-tailed test) and the number of degrees of freedom
(
= n-1).
For non-directional hypotheses, reject
if t* > +
OR if t*
< -
For directional (upper tail) hypotheses, reject
if t* > +
For directional (lower tail) hypotheses, reject
if t* < -
= 49 cm and s = 18 cm. Is this sample representative
of the known sockeye population?
1. Select the appropriate test:
You want to compare your sample mean to the known population mean - use one
sample Difference of Means test.
2. Check assumptions:
You can apply this test to your data
3. State your hypotheses:
: the sample mean is not significantly
different from the population mean (
= ): the
sample mean is significantly different from the population mean (
)
4. Select significance level:
We will use the standard = 0.05 (95% confidence
level)
5. Select probability distribution:
We will use the t probability distribution.
6. Establish your critical values:
We have non-directional hypotheses so we are conducting a two-tailed test. The
t-table accounts for the fact that the is divided
on both sides of the distribution. Therefore, we look up the full
probability at 14 degrees of freedom ( = 15-1 =
14) on the t-table. We find that =
2.15.
7. Calculate test statistic:
|
(49-60)/(18 /(sq rt 15)) = - 2.37
|
8. Compare using the decision rule:
| Rule for non-directional hypotheses: reject if t* > +
OR if t* < - t* (-2.37) is less than - (-2.15), so we
reject
|
9. State conclusion:
We conclude with 95% confidence that our sample mean is significantly different
from the population mean. Therefore, we infer that our sample is not representative
of the population.
This test calculates the difference between two sample means. This then is divided by an estimate of the standard error.
For this test, our hypotheses are:
| :
| there is no difference between the mean of sample 1 and the mean of
sample 2 ( :
1 = 2) |
| :
| there is a significant difference between the mean of sample 1 and the
mean of sample 2 ( :
1
2) |
You can also establish directional hypotheses as follows:
|
Upper tail | OR |
Lower tail |
| Formula: |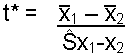 
| where: is the means from each sample is an estimate of standard error of the difference
of means
|
There are two ways to calculate the
term based on whether the variances are equal or not. Use the F test (described
under Variance Check) to assess variance equality.
1. If the variances are equal, we combine the two sample standard deviations to create a pooled ('combined') variance estimate. This pooled estimate is developed by weighting the variance of each sample by the sample size.
The formula for the pooled estimate is:
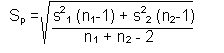
| where: s2 is the variance from each sample n is the sample size from each sample |
Use this pooled estimate to develop :
| where: Sp is the pooled variance estimate n is the sample size from each sample |
2. If the variances are unequal, you use a separate variance estimate
for :
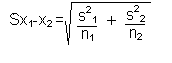
| where: s2 is the variance from each sample n is the sample size from each sample |
Note: these formulas are given so that you can better understand how SPSS is calculating the test statistic.
or
/2
and the number of degrees of freedom ( = n1
+ n2 - 2)
For non-directional hypotheses, reject
if t* > + OR if t* <
-
For directional (upper tail) hypotheses, reject
if t* > +
For directional (lower tail) hypotheses, reject
if t* < -
Hypotheses:
: the ratio of the variances
does equal 1 (s21 / s2 2 = 1 )
: the
ratio of the variances does not equal 1 (s21 /
s2 2 ≠1)
The hypotheses are non-directional for this test.
Assumption:
The population variance 
2 can be estimated
using the sample variance s2
Probability distribution:
The F test uses the F probability distribution.
Test statistic:
There are several different ways of calculating the test statistic (i.e. SPSS
uses Levene's formula which is complex). In the lab, we will use the ratio
of variances to get F*.
| Formula: |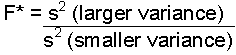 
| where: s2 is the variance (square the standard deviation to get the variance) |
Critical value:
is based on
(always for a two-tailed test, even if the t-test is 1-tail) and the
degrees of freedom n1 - 1 (larger sample size along top of F table)
and n2 - 1 (smaller sample size down left side of F table)
Click here to see online
F table
Decision rule:
Rule: reject
if F* >
= 7.3 cm, s = 1.2 cm, n=25. Sample 2 (Chemainus River) has
= 6.9 cm, s = 1.0 cm, n = 20. Do the young salmon in each
river show similar growth in their first year?
1. Check appropriate test: you want to compare two independent sample means - use two sample DoM test.
2. Check assumptions:
: s21 /
s2 2 = 1: s21
/ s2 2 ≠1
|
= 0.05, n1-1 = 24 and n2-1
= 19, = 2.11 if F*
> .
(2.11), so we do not reject .
We infer that variances are equal.
3. State your hypotheses:
| :
| there is no difference between the mean length of Goldstream salmon
and the mean length of Chemainus salmon (:
G =
C) |
| :
| there is a significant difference between the mean length of Goldstream
salmon and the mean length of Chemainus salmon (:
G
C) |
4. Select significance level:
We will use the standard = 0.05 (95% confidence
level)
5. Select probability distribution:
The population variances are unknown; we use the t distribution
6. Calculate appropriate test statistic:
Our F test showed that the variances can be considered equal, so calculate t*
using a pooled variance estimate. SPSS uses a three step calculation:
|
|
|
term:
|
|
|
:
|
|
|
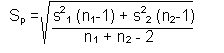
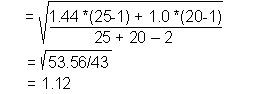
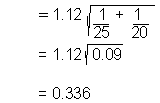
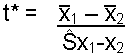
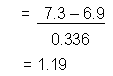
7. Identify the critical values:
At /2 = 0.025 and degrees of freedom
= 43, = 2.02
8. Compare using the decision rule:
| Rule: reject
if t* < - or t* > + t* (1.19) is less than (2.02),so we cannot reject .
| 
|
9. State conclusion:
We conclude with 95% confidence that our sample means are not different. Therefore,
we infer that the young salmon in the Goldstream and Chemainus Rivers have similar
growth in their first year.
For this test, our hypotheses are:
| : | the difference between the two means
is not different from the known or hypothesized value ( :
-  = value) |
| :
| the difference between the two means
is significantly different from the known or hypothesized value
( :
-
value) |
You can establish directional alternate hypotheses as follows:
Upper tail :
-
2 > value
| OR | Lower tail :
- 2 < value
|
Note: the known or hypothesized value could be 0 or a specific value related to the research question.
| Formula: |
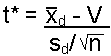
| where:d is the mean of the differences sd is the standard deviation of the differences n is the number of paired observations V is the hypothesized or known value |
The formula for the mean of differences is:
| where: is the difference between each set of paired observationsn is the number of paired observations |
The formula for the standard deviation of differences is:
| where: ( )2 is the squared difference between each set of paired observationsn is the number of paired observations |
Note: these formulas are given so that you understand how SPSS is calculating the test statistic.
or
/2 and the number of degrees of freedom ( = n-1)
For non-directional hypotheses, reject
if t* > + OR
if t* < -
For directional (upper tail) hypotheses, reject
if t* > +
For directional (lower tail) hypotheses, reject
if t* < -
| Salmon ID | Sample 1 | Sample 2 |
|---|---|---|
| Weight before hormone (kg) | Weight after hormone (kg) | |
| 1 | 4.5 | 5.6 |
| 2 | 5.0 | 5.8 |
| 3 | 4.8 | 5.8 |
| 4 | 5.2 | 5.7 |
| 5 | 4.8 | 7.2 |
| 6 | 5.8 | 7.3 |
| 7 | 4.6 | 6.0 |
| 8 | 4.9 | 6.9 |
| 9 | 4.7 | 6.6 |
| 10 | 5.1 | 6.9 |
1. Select appropriate test:
You want to compare two samples with paired observations (the samples
are not independent) - use two sample paired difference of means test.
2. Check assumptions:
You can apply this test to your data
3. State your hypotheses: Our research question: is the difference in mean weight between Sample 2 (after hormone) and Sample 1 (before hormone) greater than 0.75 kg?
To answer this question, we must use directional hypotheses. Therefore, we state:
| : | the difference between the two means
is not different from 0.75 kg ( :
2 - 1
0.75) |
| : | the difference between the
two means is significantly greater than 0.75 kg ( :
2 - 1
> 0.75) |
4. Select significance level:
We will use standard = 0.05 (95% confidence level)
5. Select probability distribution:
We will use the t probability distribution for this test.
6. Calculate test statistic:
This is a three step calculation.
| Salmon ID | Sample 1 | Sample 2 |
(Sample 2 - Sample 1) | ()2 | Calculations |
|---|---|---|---|---|---|
| 1 | 4.5 | 5.6 | 1.1 | 1.21 | Step 1: calculate d
|
| 2 | 5.0 | 5.8 | 0.8 | 0.64 | |
| 3 | 4.8 | 5.8 | 1.0 | 1.00 | |
| 4 | 5.2 | 5.7 | 0.5 | 0.25 | |
| 5 | 4.8 | 7.2 | 2.4 | 5.76 | |
| 6 | 5.8 | 7.3 | 1.5 | 2.25 | Step 2: calculate sd
|
| 7 | 4.6 | 6.0 | 1.4 | 1.96 | |
| 8 | 4.9 | 6.9 | 2.0 | 4.00 | |
| 9 | 4.7 | 6.6 | 1.9 | 3.61 | |
| 10 | 5.1 | 6.9 | 1.8 | 3.24 | |
 | 14.4 | 23.9 | |||
Step 3: calculate t*
|
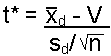7. Establish your critical values:
This is a one-tailed test because we are using directional hypotheses. Therefore,
at = 0.05 and (n-1) = 9,
= +1.83
8. Compare using the decision rule:
| Rule for upper tail hypotheses:
Reject
if t* > + t* (3.70) is greater than (1.83), so we reject
.
| 
|
9. State conclusion: We conclude with 95% confidence that the difference between
the two samples is significantly greater than 0.75 kg. Therefore, we infer that
the application of a growth hormone appears to have significantly increased
the weight of the farmed salmon (by more than the natural rate of growth).